Langton's Ant & Generalized Ant

| Counter: | |
| (From 2005/05/20) | |
|
|
Langton Multi Ant Version: 0.66
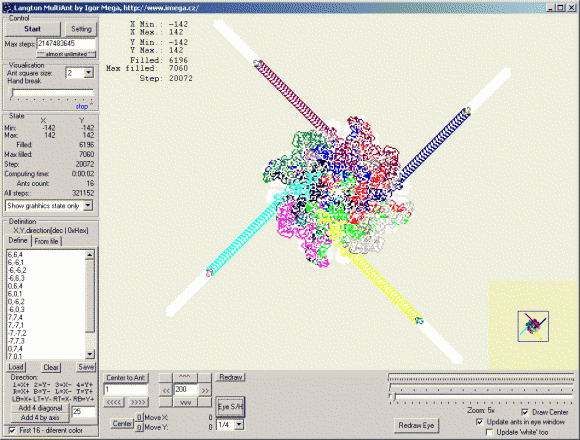
Langton's ant lives on an unbounded chessboard made initially of white squares.When he enters a square, he:
- on a white square turns right.
- on a black square turns left.
but after some 10000 steps he starts building a "highway".
That's an easy demonstration of computability problem - we know the rules applied, but we're not able to anticipate their result nor to compute it other way than step-by-step.
More ants, more fun - so:
Build your own ant-hill!!!
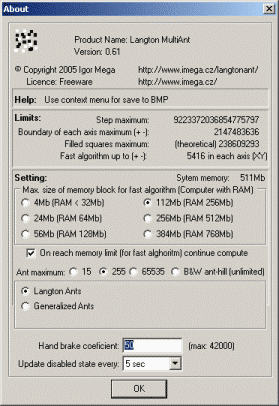
Here you have the application, which allows you to do it...You can find limits of the application in the "Setting" dialog.
They depend on your chosen setting and amount of RAM in your computer.
Even more interesting is a Generalized Ant
Squares of chessboard of Generalized Ant can have more states (colours) than just two (black x white).Generalized Ant has a program, which tells him what to do (where to turn) on a square in given state.
He doesn't simply switch the colour of the square, but increases it's state by one (and from the last allowed state back to the first one).
The ant's program is defined binary (1 = turn right, 0 - turn left) and it's length is same as number of allowed states of his universe (chessboard squares). Each bit in this program defines ant's behaviour for given state of square (place of bit corresponds to state of square - ie. on the square in the third state, third bit is used as a program).
Thus Langton's ant can be described as Generalized Ant in 2-states universe with binary program 10.
Brief help:
Definition of Langton's Ant is: StartX,StartY,Direction,Colour
- Direction - that means initial direction of ant when he enters his first square. Values LT,RT,RT,RB define direction, where the ant will start building highway to.
- Colour is optional, hexadecimal RGB colour definition used in HTML (ie. 0000FF = Red).
Definition of Generalized Ant is: StartX,StartY,Direction,Program
- Direction - that means initial direction of ant when he enters his first square.
- Program - you can enter it in binary (with Bx prefix, ie. Bx10101010 - mind that bits are used in reverse order), hexadecimal (with 0x prefix, ie. 0xAA) or decimal form (without prefix, ie. 170)
If no program is entered, default program (0xAAAAAAAAAAAAAAAA) is used (actually only first n bits, where n is number of states).
Info:
The option "B&W ant-hill" in setting dialog provides the fastest run with the widest limits applicable.
The option "Generalized" allows to run Generalized Ant in n-states universe (2-64 states) -
with this option selected, colour is used to identify a state of square (contrary to Langton's Ant, where colour identifies an ant).
Beware: if you load ants definition from a file, type of ants (Langton's or Generalized) is not included as well as number of states of Generalized Ant's universe. You must set this manually in "Setting" dialog.
TIP:
If you want to increase speed of application:
- Select "Hide state numbers" (Statistics become disabled and refreshed only each 5sec)
- "Ant square size" set to 0 (no drawing)
- Using "Eye S/H" close bird's eye window.
You can change "Hand brake coeficient" in Setting dialog, if your computer is either too slow or too fast.
For saving a picture, use context menu (right click mouse on the main graphic area).
If you want to pause, click on "stop ^"
Installation:
Download the application here (zip file)
Extract the archive (application folder will be created) and run .exe file (no installation required).
Folder contains several sample definition files (the first letter L stands for Langton's ant, G for Generalized)
Licence:
Freeware, you can distribute it even without author's permission as long as it remains unchanged.
Inspired by: Tom